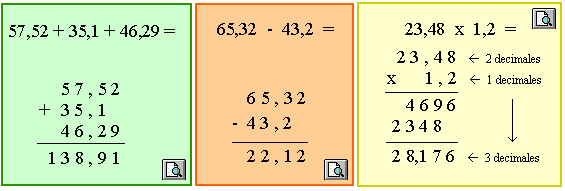Matemática
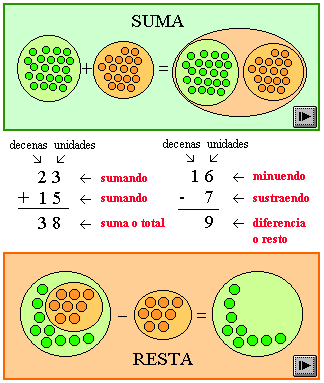
SUMA y RESTA DE NUMEROS NATURALES
i tenemos dos grupos de elementos iguales y deseamos saber cuantos tenemos en total, lo que estaremos haciendo es unir los grupos y contar los elementos del conjunto unión. A esa operación se llama suma.
|
Si de un conjunto de elementos retiramos algunos y deseamos saber cuantos quedan, lo que realizamos es una resta
|
 |
|
|
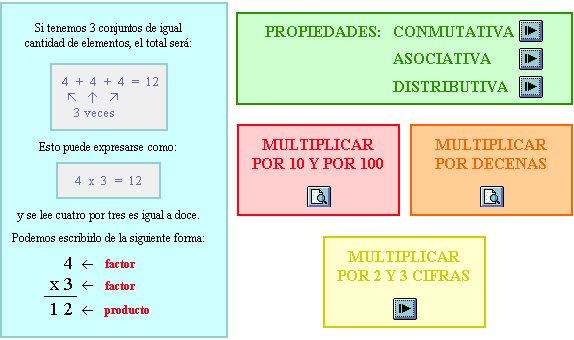
MULTIPLICACION de NUMEROS NATURALES
La multiplicación es una suma en la que todos los sumandos son iguales
|
|
|

DIVISION de NUMEROS NATURALES
| La división nos permite averiguar cuantas veces una cantidad está contenida en otra. |
|
|
|
|
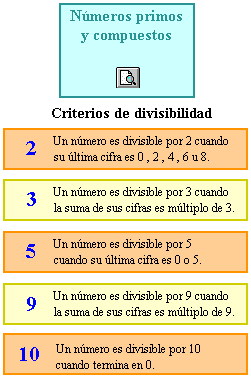
MULTIPLOS y DIVISORES
| Se llama múltiplo de un número a aquel que obtenemos al multiplicar ese número por otro cualquiera. |
|
|
Si tenemos los múltiplos de dos números, al menor número que sea múltiplo de esos dos números se lo llama mínimo común múltiplo.
|
Se llama divisor de un número a aquel que cabe en él una cantidad de veces exacta

|
Si tenemos los divisores de dos números, al mayor número que sea divisor de esos dos números se lo llama máximo común divisor.
|
|
|
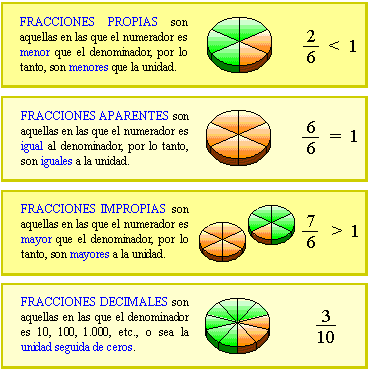
FRACCIONES
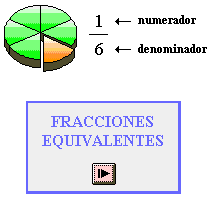
Si dividimos un objeto o unidad en varias partes iguales, a cada una de ellas, o a un grupo de esas partes, se las denomina fracción. Las fracciones están formadas por dos números: el numerador y el denominador.
|
 |
|
|
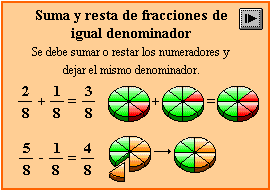
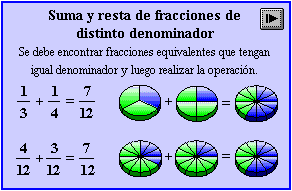
OPERACIONES CON FRACCIONES
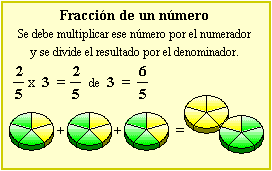
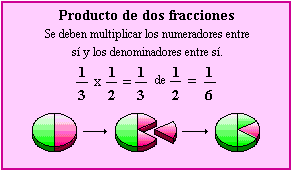
OPERACIONES CON FRACCIONES II
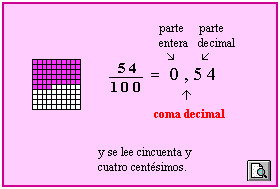
NUMEROS DECIMALES
| Los números fraccionarios decimales pueden expresarse en otra forma llamada número decimal. A su vez, los números decimales podrán también expresarse como fracciones. Las fracciones impropias están formadas por una parte entera y una parte fraccionaria. En cambio, las fracciones propias sólo tendránparte fraccionaria ya que su parte entera es igual a cero |
 |
|
|
|
|
NUMERACION DECIMAL
El sistema numérico que utilizamos para representar los números utiliza diez símbolos llamados cifras.
|
|
|
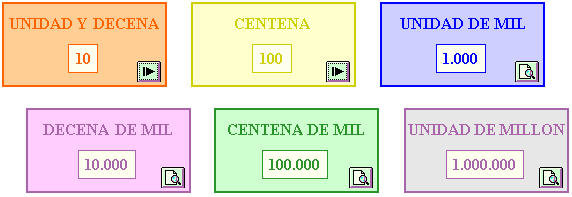
Para representar números mayores que nueve, utilizamos grupos formados por varias cifras ordenadas. La posición de cada cifra, a medida que nos trasladamos de derecha a izquierda, nos indicará las unidades, decenas, centenas, etc. Por estas razones se llama a este sistema posicional.
|
 |
OPERACIONES CON DECIMALES I
Para sumar o restar números decimales, podemos hacerlo en forma de fracción y en forma decimal.
Para sumar o restar en forma decimal se colocan los números de modo que las comas estén encolumnadas. Luego se suman o restan como si fueran números naturales, poniendo la coma en el resultado en su columna correspondiente.
Para multiplicar dos números decimales, se realiza la multiplicación de ambos como si fueran números naturales. Luego se coloca la coma en el resultado, separando tantas cifras como decimales tengan en conjunto los dos factores. |
|
|
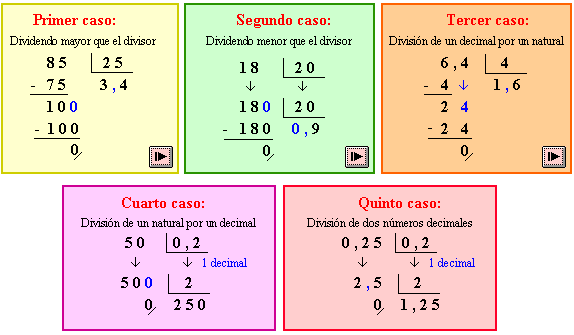
OPERACIONES CON DECIMALES II
| Las divisiones en las que participan números decimales pueden ser de varios tipos. Cada uno de estos casos se resuelve de forma diferente: |
 |
RELACIONES y FUNCIONES
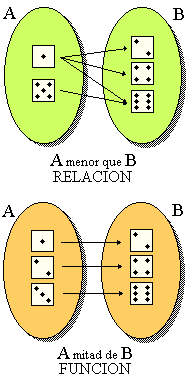
| Hay casos en que no todos los pares ordenados de un producto cartesiano de dos conjuntos responden a una condición dada. Se llama relación entre los conjuntos A y B a un subconjunto del producto cartesiano A x B. Este puede estar formado por un solo par ordenado, varios o todos los que forman parte de A x B. Si establecemos una relación entre los elementos de un mismo conjunto, existen tres propiedades fundamentales que pueden cumplirse en esa relación: propiedad reflexiva, simétrica y transitiva. |
|
|
Se llama función a una relación en la cual a cada elemento del conjunto de partida le corresponde sólo un elemento del conjunto de llegada. |
|
 |
PRODUCTO CARTESIANO
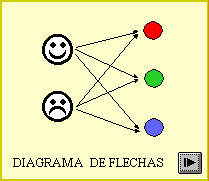
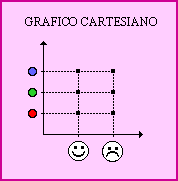
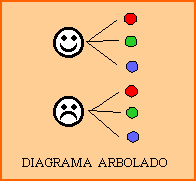
Si tenemos dos conjuntos A y B, y tratamos de armar todos los pares posibles formados por un elemento del conjunto A y un elemento del conjunto B, obtendremos el producto cartesiano de los dos conjuntos. Se escribe: 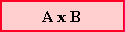 |
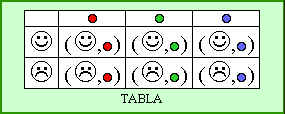
| Podemos representarlo de diferentes formas: diagramas de flechas, diagramas arbolados, tablas y gráficos cartesianos. Cada par que formemos con un elemento de A y uno de B, en ese orden, recibe el nombre de par ordenado. |
 |